オーディオ信号のリアルタイム処理では,信号はある一定の長さのフレーム(frame)毎に処理されます。フレームの長さは,システムの性能に直接影響します。例えば,出力される信号は,入力される信号に対しフレームの長さだけ遅れて出力されます。また,フレームの長さだけデータを格納しておくためにメモリが必要になります。一方,高度な処理をする場合は,フレームの長さは長くなる傾向があるでしょう。
さらに,スピーカアレイ駆動システムでは,通常のオーディオ信号の処理に加えて注意すべきことがあります。このシステムでは,集束または拡散する音響波面を発生させるため,生成する複数の信号の間に相対的な遅延時間を与えます。このため,最終的な駆動信号を生成するために複数のフレームに渡る処理が必要となってきます。この稿では,スピーカアレイ駆動システムのフレーム長について考察します。
処理の流れ
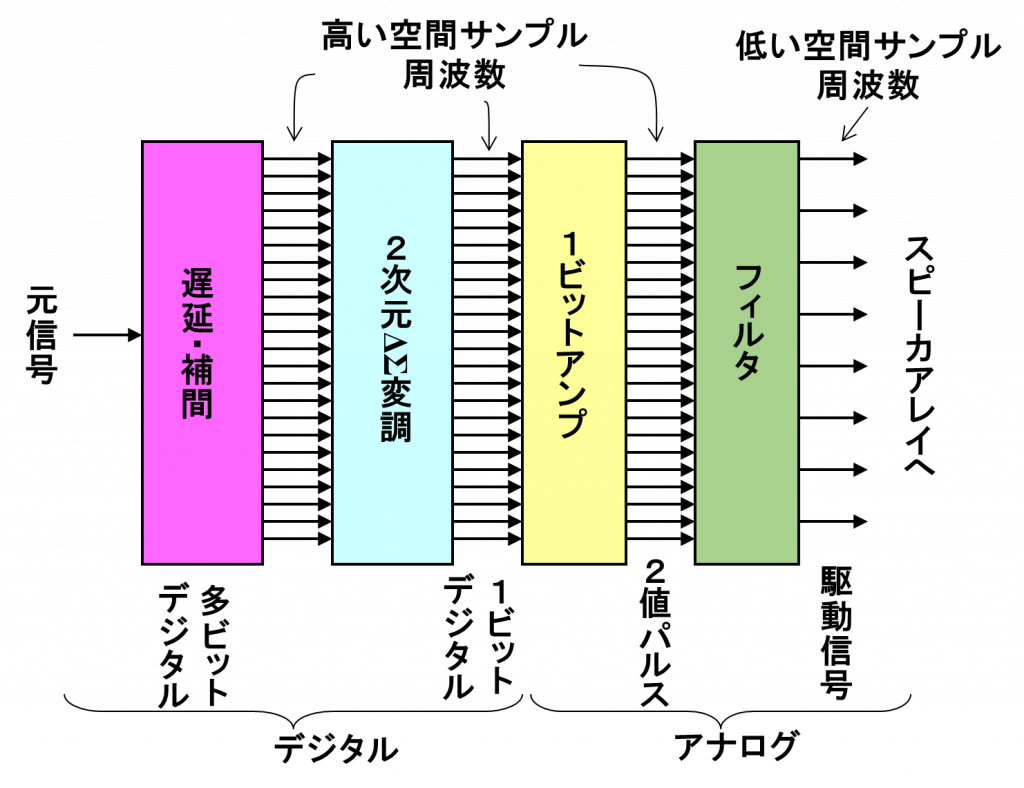
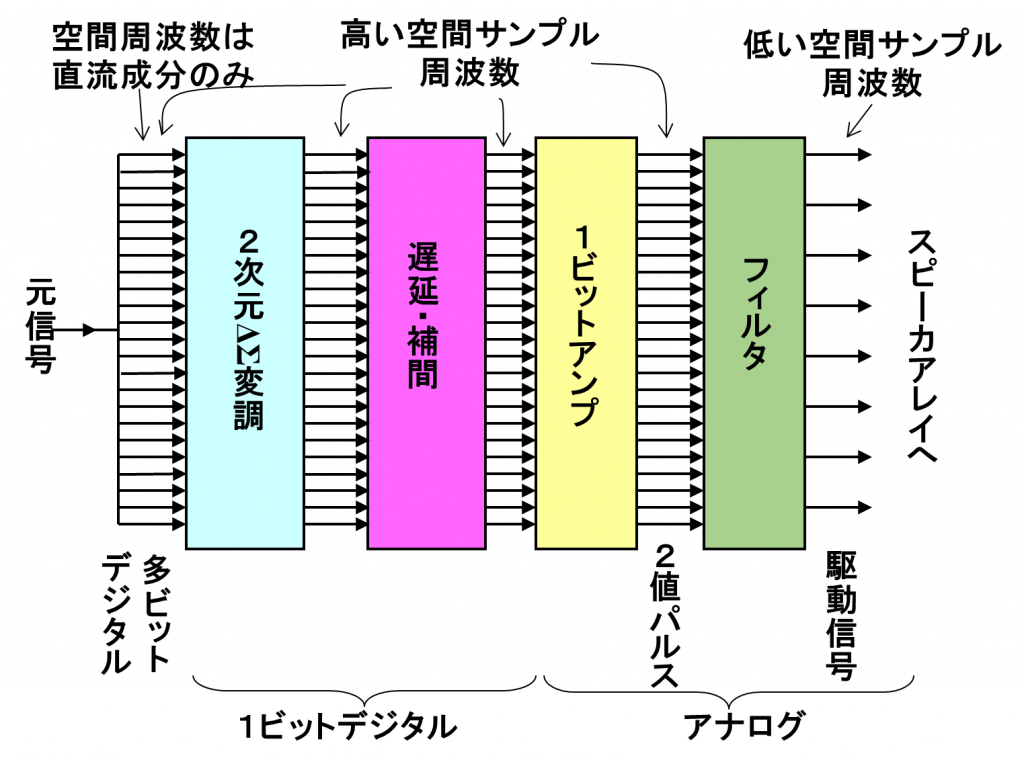
現在,二次元ΔΣ変調を用いるスピーカ駆動システムの駆動信号生成には大きく分けて2つの手法が存在します。遅延処理の後で二次元ΔΣ変調をするか,二次元ΔΣ変調後の信号に遅延処理をするか,の2つです。
- 遅延処理後に二次元ΔΣ変調
オーディオ信号に遅延を与えて,集束または拡散する波面を発生させる信号を作ります。次に,このオリジナルの信号を二次元ΔΣ変調して時間と空間の両次元に関して密な1ビットの駆動信号としています。
この構成は,オリジナルの信号を高いSN比で再現することができるというメリットがあります。一方,オリジナルの信号が高い周波数成分(空間または時間あるいは両方の次元)を持つ場合,二次元ΔΣ変調が不安定になることがあります。不安定になるとオリジナルとは全く異なる信号が生成されるてしまいます。このため,再現できる音場が制限されます。例えば,集束音場を作る際に焦点の方向の角度を大きくできなくなります。これがデメリットです。 - 二次元ΔΣ変調に遅延処理
遅延を与えない信号を二次元ΔΣ変調で変換した後で,この1ビット信号に相対的な遅延を与えて駆動信号にします。これは,安定に動作する条件下でのオリジナル信号を二次元ΔΣ変調してから,焦点形成のための遅延を与えることになります。
この方法のメリットは,どのような遅延を与えても,二次元ΔΣ変調の動作には影響がないことです。このため,集束波面の発生の場合,視野角を広く設定することができます。一方,デメリットは,再現される波面のSN比が遅延処理後二次元ΔΣ変調より低下することです。
遅延処理
遅延処理について,直線上にスピーカを配置したアレイを使い,1点に集束する音場を発生する例について説明します。
収束音場を発生させるための遅延
図のような,直線上にスピーカを配置したアレイを考えます。このアレイを含む,ある平面内の音場のみを扱うことにします。
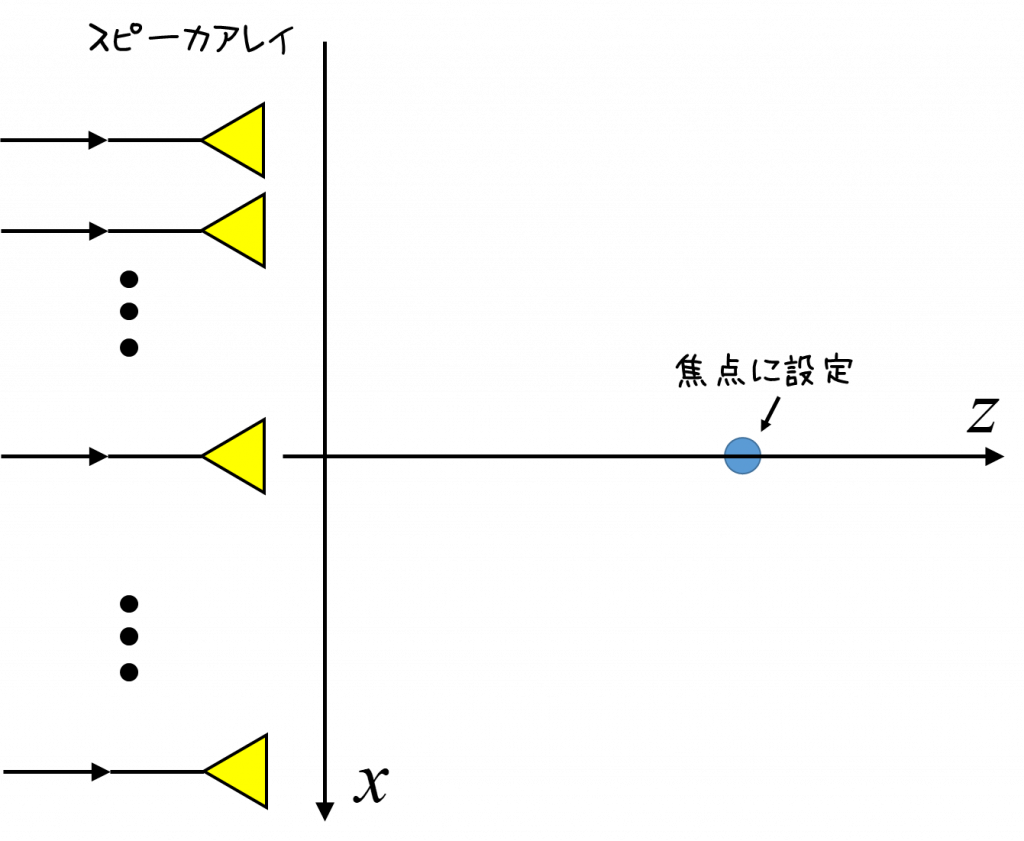
平面内の1つの点を,そこに音場が集束する点(焦点)として設定します。
以下では数式を使って説明します。スピーカが配置されている直線を![]() 軸に,アレイの中心を通り対象となる平面内に
軸に,アレイの中心を通り対象となる平面内に![]() 軸をとります。
軸をとります。![]() 番目のスピーカの
番目のスピーカの![]() 座標を
座標を![]() ,焦点の位置座標を
,焦点の位置座標を![]() とします。
とします。
①まず,はじめに,全てのスピーカを同じ信号![]() で駆動する場合を考えましょう。なお,説明を簡単にするため,波形
で駆動する場合を考えましょう。なお,説明を簡単にするため,波形![]() は,非常に短い正弦波パルスで表しています。また,波形の時間原点,
は,非常に短い正弦波パルスで表しています。また,波形の時間原点,![]() は,駆動信号の送信を始める時刻であるとします。つまり,
は,駆動信号の送信を始める時刻であるとします。つまり,![]() では信号は
では信号は
②![]() 番目のスピーカから送信され,焦点として設定した点に到達する音響波
番目のスピーカから送信され,焦点として設定した点に到達する音響波![]() は,
は,
![]()
と近似して書くことができます。ここで,![]() は,
は,![]() 番目のスピーカと焦点の間の音響伝搬時間で,スピーカの座標を
番目のスピーカと焦点の間の音響伝搬時間で,スピーカの座標を![]() ,音響波の伝搬速度を
,音響波の伝搬速度を![]() とすると,
とすると,
![]()
となります。
受信される信号は伝搬距離に応じて減衰するので,スピーカの位置により異なります。しかし,この減衰の値はほぼ一定と考えて,数式中では略しています。(詳しいことは,別稿で説明する予定です。)
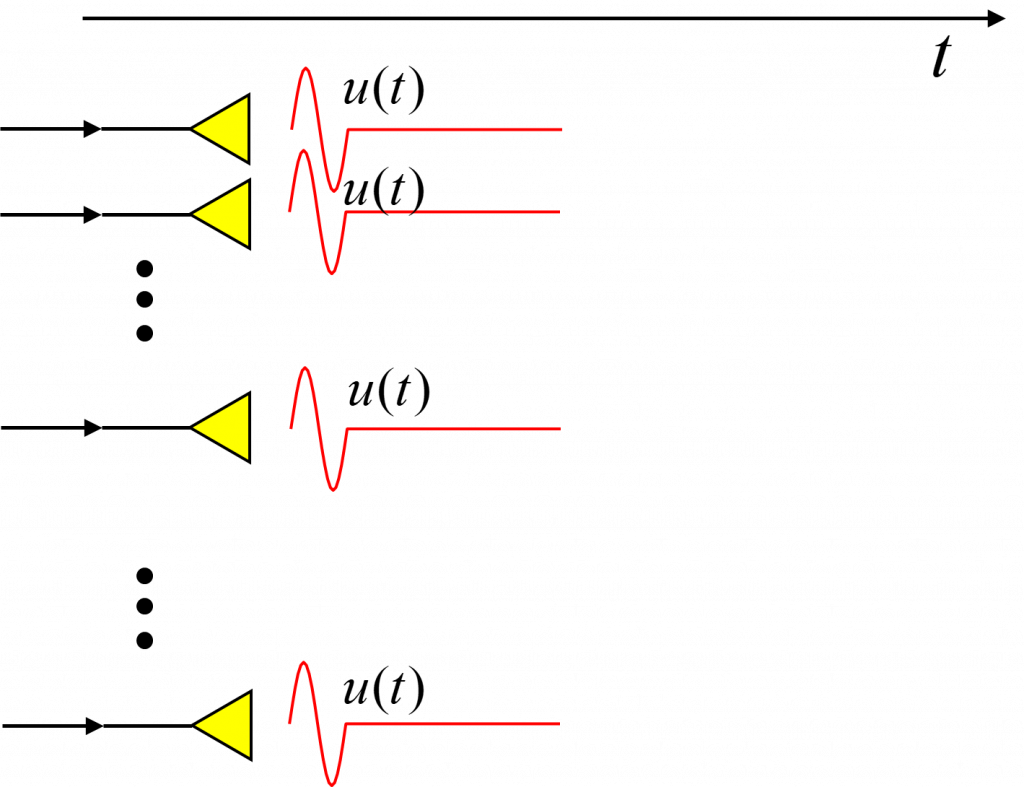
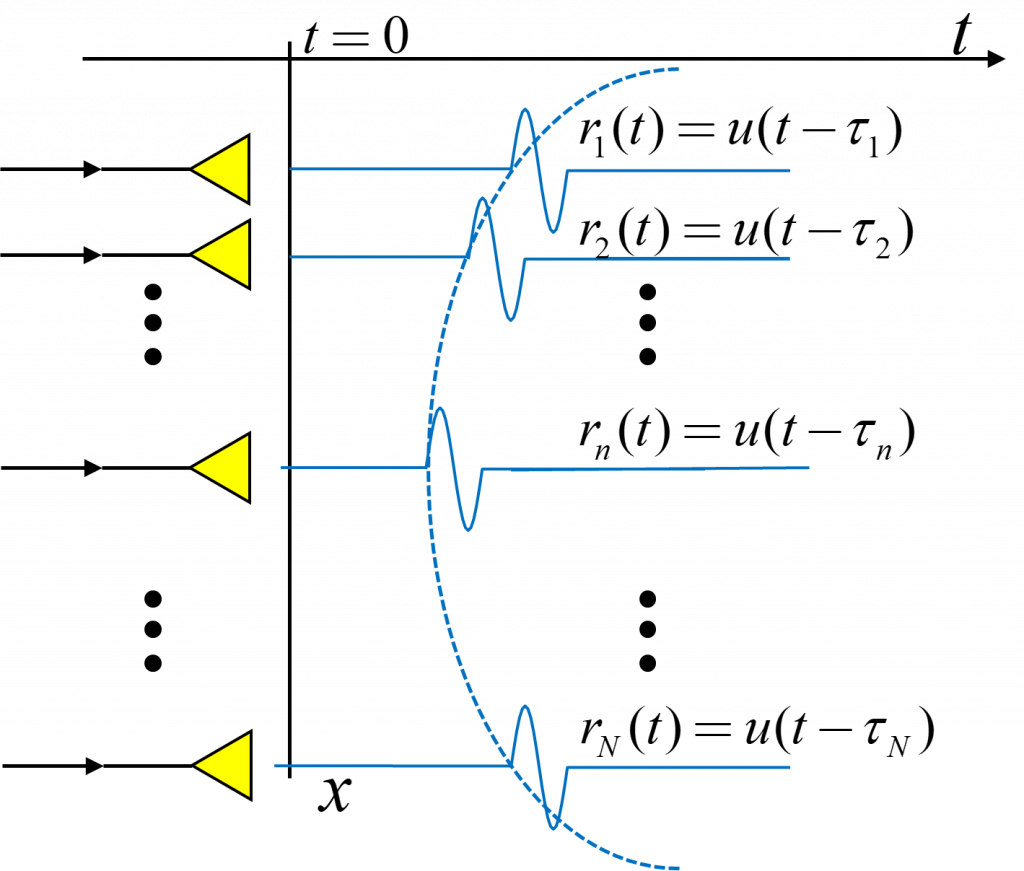
設定した点で観測される受信波は,各スピーカから到達する波形の総和になります。図の②に示したような状況では,スピーカのすべてを同じ信号で駆動すると,各スピーカから到達する信号波形は,遅延時間が互いに異なっています。このため,波形が打ち消しあって,観測される受信波の振幅は小さなものになります。
③そこで,伝搬時間を補償して送信することを考えます。![]() に対して伝搬遅延時間の符号を逆にした遅延を与えた信号を,駆動信号とします。この信号で駆動されると,各スピーカから放射され設定点に到達する音響波は,全て同じ時刻に到達します。この結果,設定された点に音響波が集束することになります。
に対して伝搬遅延時間の符号を逆にした遅延を与えた信号を,駆動信号とします。この信号で駆動されると,各スピーカから放射され設定点に到達する音響波は,全て同じ時刻に到達します。この結果,設定された点に音響波が集束することになります。
![]()
この駆動信号は![]() は,図③の赤色で表されています。これからわかるように時刻
は,図③の赤色で表されています。これからわかるように時刻![]() で値を持つので,実際には作ることができません。(時刻
で値を持つので,実際には作ることができません。(時刻![]() より前の過去に戻ることはできないので。)
より前の過去に戻ることはできないので。)
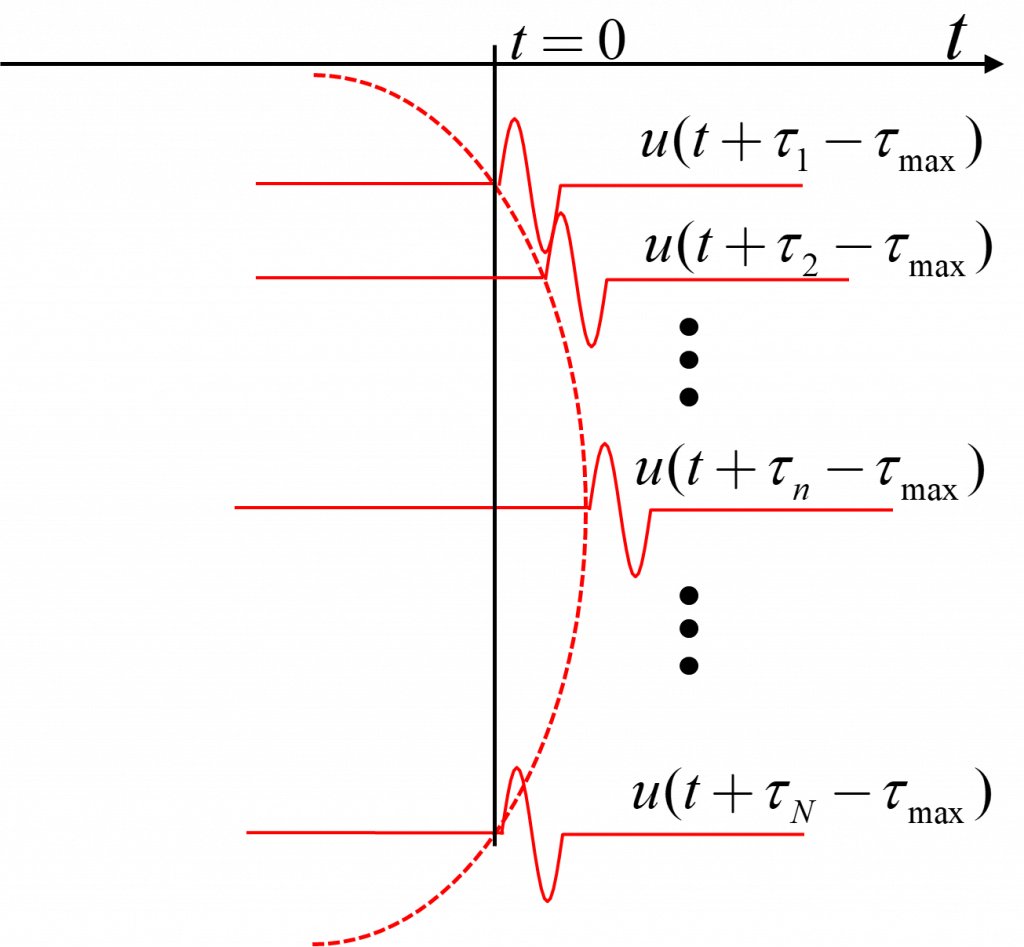
④そこで,全ての駆動信号を遅延時間![]() の最大値
の最大値![]() だけ遅延したものを駆動信号とします。
だけ遅延したものを駆動信号とします。
![]()
これらの信号の遅れ時間は0~![]() の範囲になります。ですから図④に示すように,信号の値が定義されているのは
の範囲になります。ですから図④に示すように,信号の値が定義されているのは![]() となることがわかります。
となることがわかります。

遅延の実装
信号の遅延をソフトウェアやハードウェアで実現する方法について解説します。
- 遅延線(Delay Line)
ハードウェアで実装する場合は,シフトレジスタやメモリを使った遅延線として実装すると考えやすいことがある。 - 配列のポインタ
配列に信号データを書き込んでおき,それを読み出すことで遅延を実現できる。MATLABやC/C++言語を使って設計する場合は,配列の添え字(インデックス)やポインタを操作することで,遅延された信号を生成する。
現在のシステム構成では,信号を発生する部分はMATLABを使っています。そこで,これ以降では,配列を用いる方法について説明していきます。
条件は以下のとおりです。
- 二次元ΔΣ変調後遅延を想定
フレームのデータは二値に変換され時間的にオーバーサンプルされている。本研究ではサンプリング周波数は3MHzとしている。なお遅延に関しては,データが二値化されていないことを除き,二次元ΔΣ変調後遅延方式と遅延後二次元ΔΣ変調方式とでは同じ処理になる。 - フレーム長は最大遅延
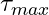 より長いものとする
より長いものとする - 出力信号のフレームも同じ長さとする
この遅延処理は,二次元ΔΣ変調で得られたデータを入力とし,出力される信号(駆動信号)は入力と同じ長さのフレーム単位で出力されるものとする。
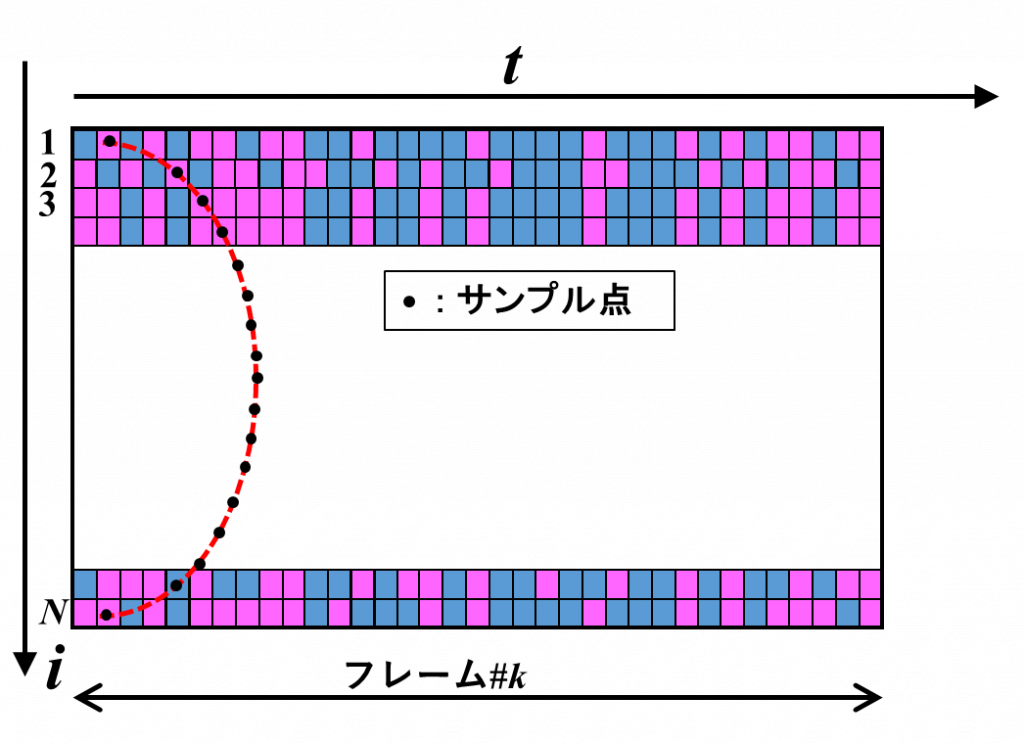
出力フレームは,入力フレームの配列から,集束のための遅延![]() に応じて計算されたインデックスでサンプルした値を並べたものになっています。図の①は,出力フレームの最初のデータを作る処理を表しています。入力フレームは2次元配列の形になっています。赤色の点線は入力フレームの最初のインデックス(左端を指しています)から
に応じて計算されたインデックスでサンプルした値を並べたものになっています。図の①は,出力フレームの最初のデータを作る処理を表しています。入力フレームは2次元配列の形になっています。赤色の点線は入力フレームの最初のインデックス(左端を指しています)から![]() だけ遅らせたものを表しています(以下,“サンプルライン”と呼ぶことにします)。赤い線の上の黒丸が,値をサンプルする位置を示しています。
だけ遅らせたものを表しています(以下,“サンプルライン”と呼ぶことにします)。赤い線の上の黒丸が,値をサンプルする位置を示しています。
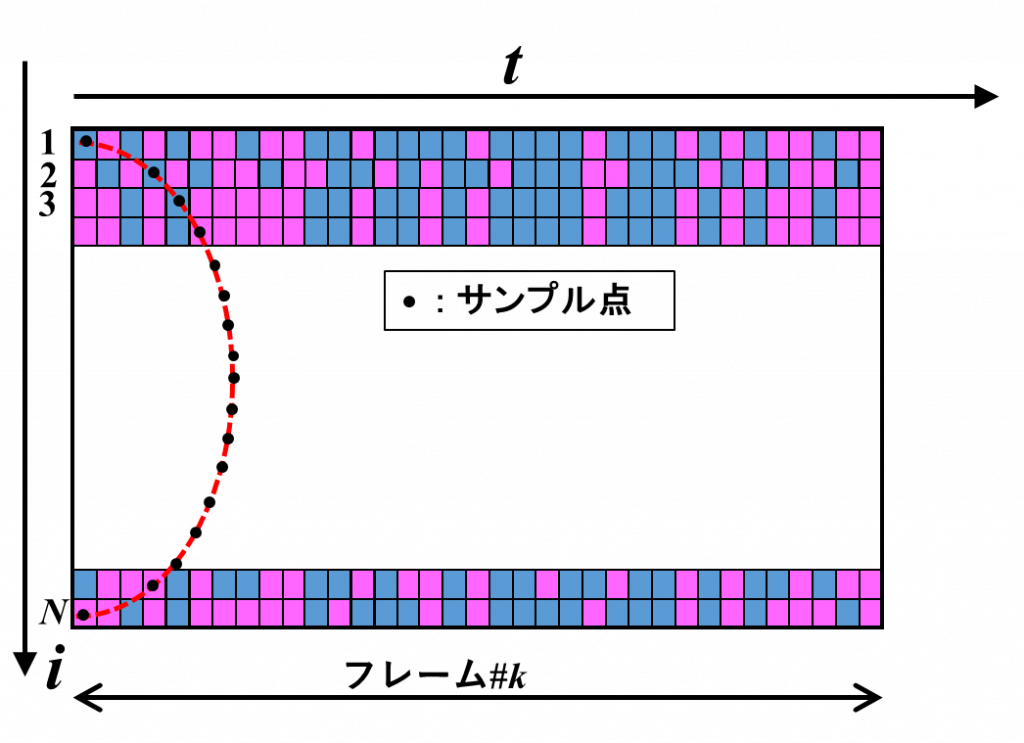
出力フレームの第2サンプルの値は,図②のように,サンプルラインを1つ右にシフトしてサンプルしたデータになります。
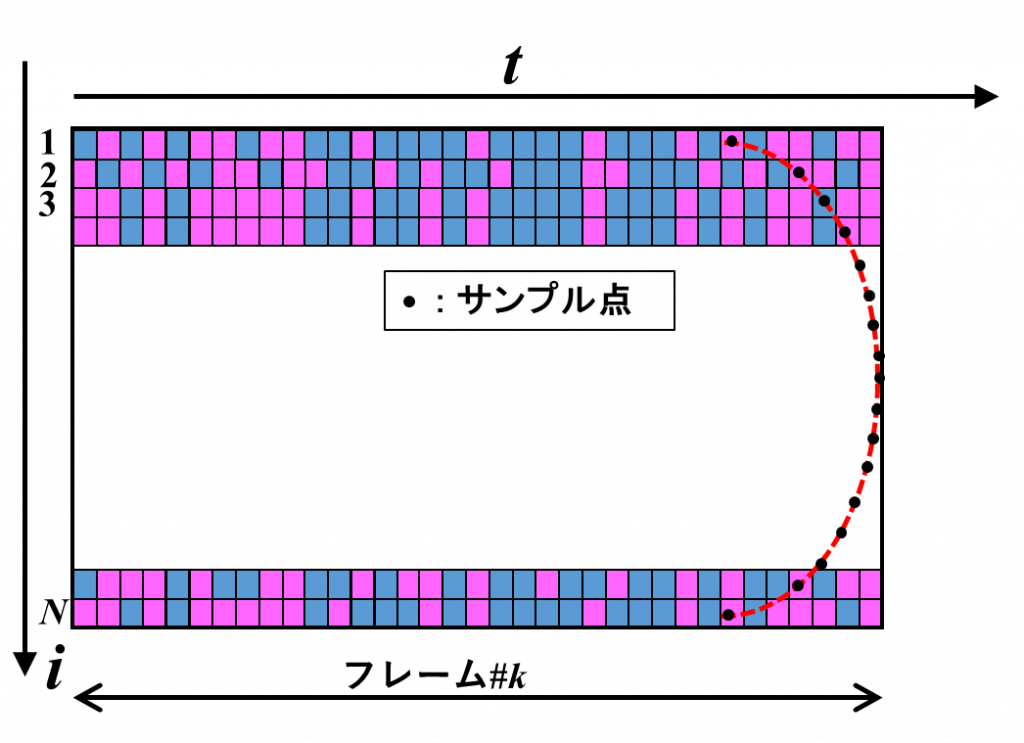
以上のようにして第3サンプル,第4サンプル,・・・とサンプルラインをシフトしながら出力フレームの値を求めていくと,サンプルラインが入力フレームの右端に到達した状態になります。1つの入力フレームから計算できるのは,ここまでとなります。
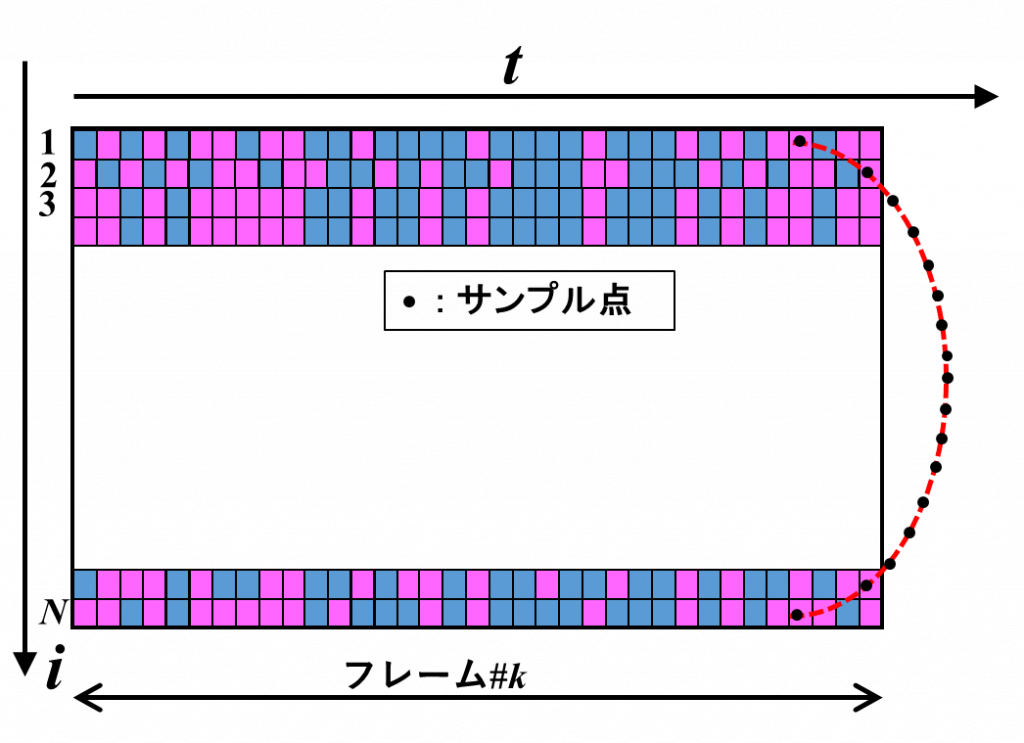
図④は,出力フレームの③の状態よりも後ろのサンプル値を求める場合のサンプルラインを示しています。サンプルラインは入力フレーム(![]() 番目のフレームとしている)をはみ出し,次の
番目のフレームとしている)をはみ出し,次の![]() 番目のフレームにかかっています。
番目のフレームにかかっています。
この説明では,フレーム長は指向性形成のための遅延の最大値![]() より大きいことを想定しています。したがって,1つの出力フレームを計算するためには,2つの入力フレームが必要であることになります。
より大きいことを想定しています。したがって,1つの出力フレームを計算するためには,2つの入力フレームが必要であることになります。
フレーム長が![]() より小さい場合は,3つ以上の入力フレームが必要になります。しかし,ここではフレーム長が
より小さい場合は,3つ以上の入力フレームが必要になります。しかし,ここではフレーム長が![]() より大きい場合について説明します。
より大きい場合について説明します。
数値例
次の条件で遅延量の最大値を計算してみる。
- スピーカアレイの寸法
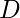 :直径1m
:直径1m - 収束点のアレイ主軸からの角度の最大値:
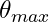 = 30°
= 30° - 音速 :
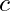 = 340m/s
= 340m/s
遅延量の最大値の概略値は,
![]()
![]()
となり,1.47msとなることがわかります。したがって,フレーム長は1.47ms以上となり,出力までは2フレーム分の遅延となるので,最低2.94msのレイテンシの処理になります。


コメント